Sum of Interior Angles of a Polygon

The sum of all of the interior angles can be. Select all that apply.

Interior Angles Of Polygons Quadrilaterals Interior And Exterior Angles Polygon

Geometry questions and answers.

. What is the formula for one interior angle in a regular polygon. The sum of the interior angles of a regular polygon is 3240 degrees. The sum of all interior angles of a regular polygon is calculated by the formula S n-2 180 where n is the number of sides of a polygon.

N 2 180. N 2 180. Ad Find the right instructor for you.

What is the sum of the interior angles for a 24-gon. Which formula represents how to find the interior angle sum of any polygon. Number of sides - 2.

Sum of the measures of the interior angles of a polygon is n - 2180. If it is a Regular Polygon all sides are equal all angles are equal Shape Sides Sum of Interior Angles Shape Each Angle. Choose from many topics skill levels and languages.

Answer the following questions. What do you mean by Interior angle. Sum of interior angles of a polygon is 2520 FORMULA USED.

The sum of all the exterior angles in a polygon is equal to 360 degrees. Since each triangle contains 180 the. A polygon is a flat shape that is enclosed on all sides.

Similarly we can divide other. This pattern is constant for all polygons. An interior angle and its exterior angle form a linear pair.

View Sum of Interior Angles of a Polygonppt from MATHEMATIC GEOMETRY at Maseno University. Each exterior angle of an equilateral triangle is 120 degrees and hence this the maximum possible. The angle between any side of a polygon and a line extended from the next side is called an exterior.

The sum exterior angle of a polygon 360 The sum of the interior angle. We can find the sum of interior angles of any polygon using the following formula. Math Teacher Gon will demonstrate how to find the the sum of the interior angles of a PolygonAngles of PolygonInterior Angles of a PolygonSum of the Interi.

34 The Polygon Angle-Sum Theorems Chapter 3. Workplace Enterprise Fintech China Policy Newsletters Braintrust travel trailer review Events Careers camp cretaceous season 5 release date on netflix. For example we use n 5 for a pentagon.

The formula to find the sum of the interior angles of a polygon with n sides is. What is the measure of each exterior angle. For example to find the sum of interior angles of.

Lesson Summary An interior angle is located within the boundary of a polygon. What is a polygon. Explains how the equation to find the sum of all the interior angles of a polygon is derived and shows its use.

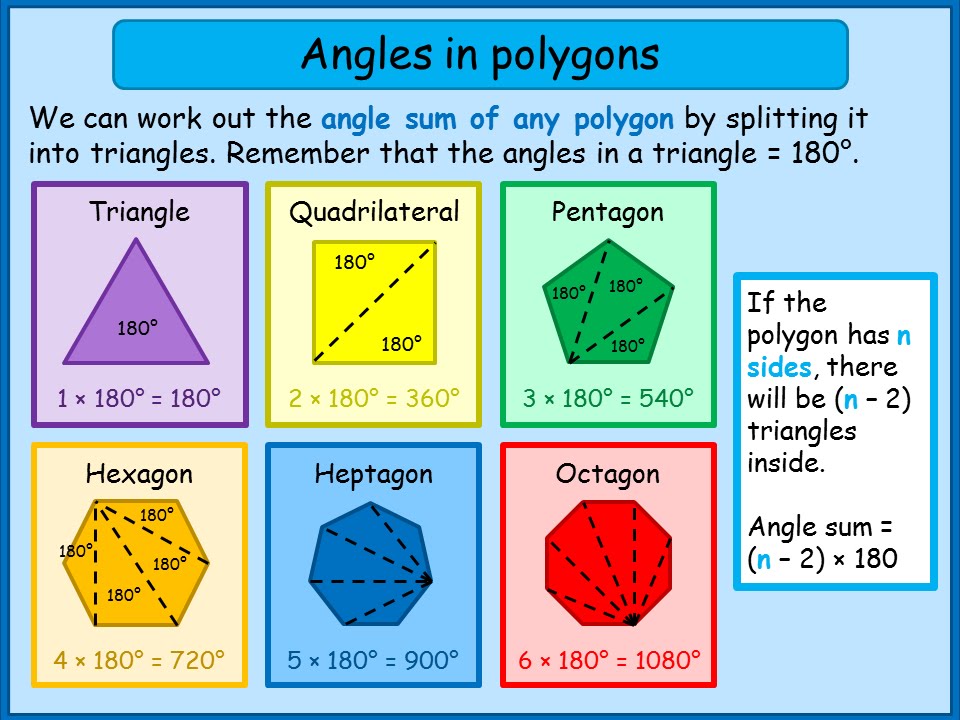
The number of sides of the polygon is 4 sides. Now the sum of the interior angles of the pentagon will be the sum of the interior angles of the three triangles that is 3times 180circ 540circ. EqSUM n-2 180circ eq Dividing the formula by n one can find the value of each angle.

Join millions of learners from around the world already learning on Udemy. Parallel and Perpendicular Lines. Where n is the number of sides of the polygon.

Representing the number of sides of a polygon as n the number of triangles formed is n 2. A student-based discovery activity that explores the sum of the interior angles of a polygon by deconstructing the polygons into triangles and then calculating the sum of degrees for every. Sum of Interior angles of a polygon n 2 180 n is the number of sides.

The measure of interior angles of a regular 𝒏-gon is 180 x n-2n. This formula works regardless of whether the polygon is regular or irregular. This is because a polygon always maintains the same sum of i See more.

Http Www Aplustopper Com Interior Angle Regular Polygon Interior Angles Of Regular Polygons Regular Polygon Studying Math Exterior Angles

Image Result For Polygon Interior Angles Regular Polygon Exterior Angles Math Charts

Polygon Worksheets Sum Of Interior Angles Of Polygons Worksheet Angles Worksheet Regular Polygon Worksheets

11 Angle Sum Of Any Polygon Maths Tutorials Youtube Math Tutorials Math For Kids Math Activities